臨床に役立つ浸透圧、電解質濃度計算【mol/L, mOsm/L, mEq/L】

本記事では「浸透圧及び電解質濃度計算」について簡単な例題、臨床での使用例を踏まえながら分かりやすく解説します。

きっかけとしては質問箱にてミオテクターのK⁺濃度補正の質問がありMoegiが返答しました。

【質問箱より】mEq/Lの計算式について教えてください！

【質問への回答】

臨床/看護の現場と計算問題について

臨床工学技士の国家試験において、受験生が苦手とする代表科目が電気・電子工学、機械工学、流体力学 etc….・・・と、言い出したらキリがないのですが、計算問題を苦手とする学生さんや実習生をよく見かけます。

そして、中でも型通りにすれば解けるのですが、特に公式といったものがない「浸透圧」や「電解質濃度」に関しての問題を苦手とする人が多い気がします。

学生さんに関わらず、今回の濃度補正の質問があったように、新人CEさんも、学生の間苦手としたままCEとなった方も大勢いらっしゃるハズです。

国試を解いてて、「こんな計算、実臨床では使わないから捨てる！！」としてきた方もいらっしゃるかと思いますが、いえ、普通に使用しますよ。

ミオテクターの電解質補正、サブラッドのNa⁺補正、PEの置換液の電解質補正など業務で計算を行います。

あとは個人の勉強として、例えば「アルブミン置換のPEで、徐々に血圧が下がる傾向にあるな・・・。アルブミン製剤のNa⁺濃度って[mEq/L]でどうなんだ？」と調べる方もいらっしゃることでしょう。

当記事では学生さん、新人さん向けに1から説明したいと思います。

ちなみにですが、私Moegiは数字には滅法強い方で、その場でパッと暗算なり手計算ができるタイプです。そういえば、編集部や友人から「ようそんなその計算脳持っとるなぁ。」的なことを言われた記憶あります。

ちょっと変わった角度から考えたり、やりやすいコツなどを見つけるのが得意ですので、是非参考にしていただきたいと思います。

モル [mol]について

モル[mol]とは　ー物質量の単位ー

計算上というよりも、高校の化学や物理の時から「何やモルって、意味わからん！！」ってなっていた方が多いと思います。

医療安全管理学のボンベの問題だったり、それこそ電解質濃度計算には必要な考えだったりしますので、まずは「モル[mol]」から説明します。

今回はモルについて詳しく説明しておきます。
ここが一番重要です。

モル[mol]とは物質量の単位なのですが、イメージしにくいんですよね・・・。
順に説明します。

1[mol]とはどんな物質量なのかと言いますと、

ある特定の原子あるいは分子が6.02×10²³個集合した時の量

を示しています。この6.02×10²³をアボガドロ定数（アボガドロ数）といいました。

さて、これだけでは今回は特に意味は無く、次に説明する「モル質量[g/mol]」が意味を成してきます。

モル質量[g/mol]

モル質量[g/mol]についてですが、簡単に表現すると「分子量の単位」です。

原子量と分子量というのがありますが、モル質量[g/mol]で表すならば、例えば水素 Hは原子量1[g/mol]、ナトリウム原子 Na は23[g/mol]です。
分子量では、例えば水分子 H₂Oは18[g/mol]、グルコース C₆H₁₂O₆は180[g/mol]です。

つまりは、ある原子または分子（分子量x[g/mol]）を6.02×10²³個集めた物質の重さは、いかなる物質でも分子量x[g]となるのです。

例に挙げた4つの1[mol]物質の重さは、ナトリウム原子 Na は23[g]、水分子 H₂Oは18[g]、グルコース C₆H₁₂O₆は180[g]となるのです。

・・・安心してください、原子量、分子量は問題文に明記されますので、覚えるに越したことはないのですが、覚えなくて良いです。

気体定数について

例題【モル[mol]】

例題を解いていきましょう。

徐々に難しくしていきます。

まずはシンプルに。
CO₂の分子量は44[g/mol]なので、88/44=2.0[mol]です。

次は少しリアリティな数字を想定しました。
C₆H₁₂O₆の分子量は180[g/mol]なので、25/180≒0.139[mol]
設問は[mmol]ですので、0.139[mol]＝139×10^-3[mol]=139[mmol]となります。

生食のNaCl濃度は0.9%ですので、生食1[L]中にはNaClは9.0[g]となります。
NaCl分子量は23+35.5＝58.5[g/mol]です。
ですので、生食1[L]中NaClは9.0/58.5≒0.154[mol/L]

同様に単位変換をし、NaClは154[mmol/L]
したがって、イオン化したNa⁺も154[mmol/L]となります。

標準状態の気体の体積は物質量[mol]×22.4[L/mol]で求められますので、
10×22.4=224[L]となります。

本項最終問題です。
ボンベ内のCO2は液体です。CO₂ 8.8[kg]は8800/44=200[mol]です。
よって、200×22.4=4480[L]です。

ミリ当量[mEq/L]について

ミリ当量[mEq/L]とは何か

本ブログで重要なのは前項のモル[mol]ですが、今回のメインは本項のミリ当量[mEq/L]ではないかと思います。

[mEq/L]の単位自体は血ガスや採血結果で嫌ほど毎日見かけてる方は多いのではないでしょうか。

まず単位自体の話をします。
[mEq/L]は電解質の濃度を表す単位であり、溶液中1[L]の溶質のミリ当量を示しています。

【Eq】は【equivalent】の略で「イクイヴァレント」と読み、当量を意味します。

ですので、[mEq/L]の読み方は「ミリ イクイヴァレント パー リットル」と言うか、単に「メック」と言います。後者の方が多いのではないかと思います。

ミリ当量の換算方法は

「ミリ当量」ということですが、単位は以下の関係にあります。

[mEq/L]　＝　[mmol/L]　×　[電荷数]

基本的に扱うのは、K⁺やNa⁺、Cl^–などの電解質が1価ですので、無意識に問題なくやり過ごしてしまっている可能性があるのですが、Ca²⁺やMg²⁺の際は単位変換時に2倍、もしくは半減する必要があるのです。

例えば、K+は1価陽イオンのためK+ 1[mmol]は1[mEq/L]へ、Ca²⁺は2価陽イオンのためCa²⁺ 1[mmol]は2[mEq/L]へと単位変換となります。

忘れがちなので何度も言いますが、[mmol/L]から[mEq/L]の変換は、イオンの荷電数に注意しましょう。
[mol/L]ではなく[mmol/L]ですのでこちらもご注意ください。

また、グルコースやBUNなど電解質以外には使用できない単位です。

[mEq/L]に関しては[mmol/L]からの単位変換の話ということなのでこれで終了です。
例題にいきましょう。

例題【ミリ当量[mEq/L]】

シンプルに、Na⁺は1価陽イオンであるため、数字そのままの154[mEq/L]です。

まず、モルでを求めます。
9.0[mg/dL]=90[mg/L]=90×10^-3[g/L]です。（単位変換）

したがって、90×10^-3/40=2.25×10^-3[mol/L]となります。（血清総Caのモル濃度）

このうち50%がイオン化しているので、Ca²⁺のモル濃度は
2.25×10^-3×0.5＝1.125×10^-3[mol]=1.125[mmol]となります。（敢えて四捨五入していません）

よって、Ca²⁺は2価陽イオンですので1.125×2=2.25[mEq/L]となります。

例題3が利用できます。（途中まで全く同じですが、一応記載します。）

生食のNaCl濃度は0.9%ですので、生食1[L]中にはNaClは9.0[g]となります。
NaCl分子量は23+35.5＝58.5[g/mol]です。
ですので、生食1[L]中NaClは9.0/58.5≒0.154[mol/L]

同様に単位変換をし、NaClは154[mmol/L]
したがって、イオン化したNa⁺も154[mmol/L]となります。

よって、Na⁺は１価陽イオンですので154[mEq/L]となります。

さて、少し前の国試から出題です。
正答率は低かったのではないかと考えますが、もう解けるでしょう。

CaCl₂の分子量は111[g/mol]です。
単位変換をすると、1110[mg/dL]=11100[mg/L]となるので、CaCl₂のモル濃度は
11100[mg/L]/111[g/mol]=100[mmol/L]となります。

CaCl₂がイオン化するとCaCl₂→Ca²⁺＋2Cl^–です。

わかりやすくするために次の2行を加えますが
Ca²⁺について2価陽イオンのため、100×2＝200[mEq/L]、
Cl^–について、2倍あるため100×2＝200[mEq/L]となりますので、
結果的に当量濃度は200[mEq/L]となります。

浸透圧 [mOsm/L]について

浸透圧の単位mOsmについての解説

いよいよ最終項目の浸透圧 [mOsm/L]です。

まず単位の読み方ですが、【Osm】は【Osmole】の略で「オスモル」と読みます。
通常、浸透圧の世界では、「ミリオスモル」の[mOsm/L]が使用されます。

何故、[mOsm/L]が最後の解説なのかといいますと、一番間違えやすいからです。

さて、浸透圧は簡単に言い表すと、「水を引き込む力」のことですが、浸透圧[mOsm/L]を考える際には水1[L]中の「分子」や「イオン」の数・・・言い換えると「粒子」の数で決まります。

[mEq/L]はイオン化する電解質しか対応しませんでしたが、浸透圧[mOsm/L]ではイオンに加え、グルコースやBUNなどの分子も含めて考えることができます。

大事なことなので2度言います、いえ何度でもいいます。
浸透圧[mOsm/L]は「粒子」の数です。
「粒」の数です。

どういうことかと言いますと、例えばNaCl溶液があります。
1[L]中にNaClが1[mmol]溶解しているとすると、分子としてはNaCl 1[mmol]ですが、イオンとしてはNa⁺ 1[mmol]、Cl^– 1[mmol]ずつ存在するので、「粒子」としては2[mmol]のイオンが存在します。

よって、上記NaCl溶液の浸透圧は2[mOsm/L]となります。

浸透圧 [mOsm/L]で間違いやすいポイント

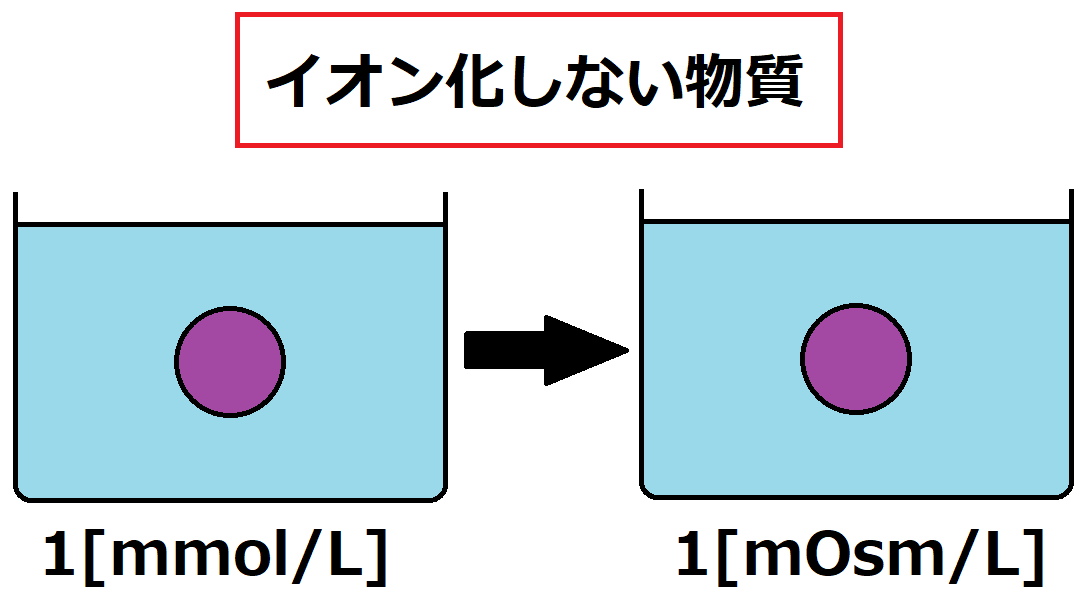
基本的には、[mmol/L]=[mOsm/L]が成立しますが、この時の[mmol/L]は「粒子の合計」です。

グルコースやBUNなどのイオン化しない物質の浸透圧 [mOsm/L]はモル濃度[mmol/L]に等しいです。
下図の通り、粒子が1[mmol/L]なら浸透圧も1[mOsm/L]となります。

しかし、イオン化する物質の浸透圧[mOsm/L]ではこうはいかないのが、苦手とする人が多い理由でしょうか。

例えば塩化カルシウムCaCl₂水溶液1[L]があります。
1[L]中にCaCl₂が1[mmol]溶解しているとすると、分子としてはCaCl₂ 1[mmol]です。
となるとイオンとしてはCa²⁺ 1[mmol]ですが、Cl^– は２[mmol]ずつ存在するので、「粒子」としては合計3[mmol]のイオンが存在することになります。

というわけで、上記のCaCl₂水溶液の浸透圧は3[mOsm/L]となります。

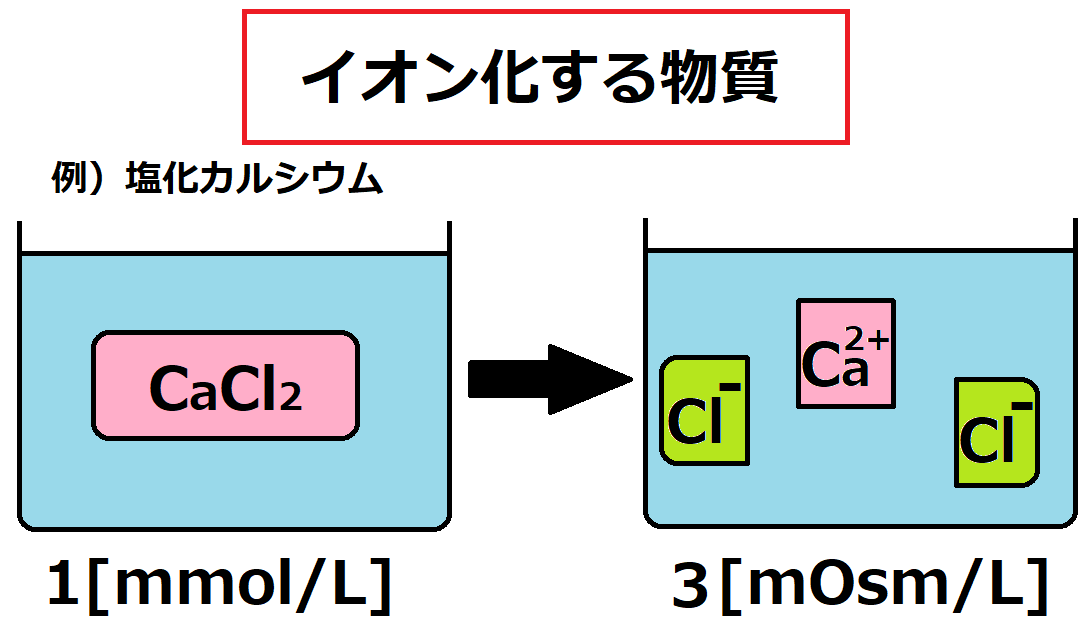イオン化する物質の溶液の浸透圧を考えるとき、陽イオン：陰イオン＝1：1なのか、1：2なのか、はたまた1：3なのかをしっかり見逃さないことがポイントとなります。

例題 【浸透圧[mOsm/L]】

例題2を利用しましょう。

C₆H₁₂O₆の分子量は180[g/mol]なので、25/180≒0.139[mol]
設問は[mmol]ですので、0.139[mol]＝139×10^-3[mol]=139[mmol]となります。
これが500[mL]に溶けているので、139[mmol]/0.5[L]＝278[mmol/L]です。

グルコースはイオン化しない物質ですので、浸透圧は278[mOsm/L]となります。

こちらは例題3と8を利用します。

生食のNaCl濃度は0.9%ですので、生食1[L]中にはNaClは9.0[g]となります。
NaCl分子量は23+35.5＝58.5[g/mol]です。
ですので、生食1[L]中NaClは9.0/58.5≒0.154[mol/L]

同様に単位変換をし、NaClは154[mmol/L]でイオン化する物質ですのでイオン化したNa⁺もCl^–も共に154[mmol/L]となります。

浸透圧は粒子の数でしたので、浸透圧は154+154=308[mOsm/L]と求まります。

さて、例題9の国試過去問改です。

CaCl₂の分子量は111[g/mol]です。
単位変換をすると、1110[mg/dL]=11100[mg/L]となるので、CaCl₂のモル濃度は
11100[mg/L]/111[g/mol]=100[mmol/L]となります。

CaCl₂がイオン化するとCaCl₂→Ca²⁺＋2Cl^–です。

クドい様ですが、浸透圧は粒の数ですので、
Ca²⁺については、そのままの数字で100[mOsm/L]、
Cl^–については、2倍あるため100×2=200[mOsm/L]となりますので、CaCl₂水溶液の浸透圧は300[mOsm/L]となります。

では最終問題とします。ME2種の過去問です。

まず、モル濃度から求めます。
10%食塩水1[L]を想定すると、溶解している食塩の量は100[g]、つまり100[g/L]。
モル濃度は100[g/L]/58.5[g/mol]≒1.71[mol/L]となります。

NaClはイオン化するため、Na⁺もCl^–も共に1.71[mol/L]となります。
よって、10%NaCl溶液は1.71×2=3.42[Osm/L]です。

普段使用する単位にすると、3420[mOsm/L]ですので、かなり高等張となりますね。
そりゃ、透析で血圧下がった時に投与したら昇圧しますわ・・・。

臨床での応用例　輸液のmOsm/Lの計算とその重要性

オススメの参考書

これらの例題の他にももっと電解質について学んでみたい方におすすめの参考書をいくつか紹介します。

水・電解質・酸塩基平衡クイックリファレンス

日常的に水・電解質・酸塩基平衡異常はしばしば遭遇します。
電解質異常のタイプごと解説、遺伝性疾患など鑑別ポイントも網羅されています。
研修医から専門医向けですが、役に立つ1冊と思います。

電解質輸液塾 改訂2版

電解質が苦手な方にオススメの参考書です。
原理と原則から徹底的に叩き込むことを優先し、簡潔にわかりやすく解説されています。
電解質異常の基礎から学べる1冊です。

ハルペリン 病態から考える電解質異常

水・電解質,酸塩基平衡の英語の世界的教科書「Halperin」は、具体的な症例をから水電解質、酸塩基平衡異常を病態から解き明かすことで、診断と治療に結びつけ解説した名著です。
かなり読み応えのある本です。

きどにゃんとゆく!水・電解質を学ぶ旅 腎生理がわかれば、水・電解質異常がわかる! 

水・電解質異常を腎生理から学ぼうとする参考書です。
腎臓の進化から腎生理を学び、豊富なイラストと図表で解説されています。
腎臓のこともついでに学びませんか？

さいごに

以上で、[mol/L]、[mEq/L]、[mOsm/L]などの皆さんが苦手とする計算問題に関する解説でした。

誘導問題のような形式で、例題問題解く事で理解が深まったかと思われます。

透析や集中治療、人工心肺業務の計算でお役立てていただければ嬉しいです。